Teoría de Shannon
Es un modelo matemático orientado a las comunicaciones que tenia sus propósitos eran enfocados en la transmisión de información, estos eran.
- Mejorar la velocidad en la creación y transmisión de mensajes.
- Mejorar la capacidad de canales de comunicación.
- Obtener una codificación eficaz de los mensajes, que evite el ruido e interferencias entre emisor y receptor, este lenguaje informático es uno de los más eficaces. [1]
Modelo de Shannon
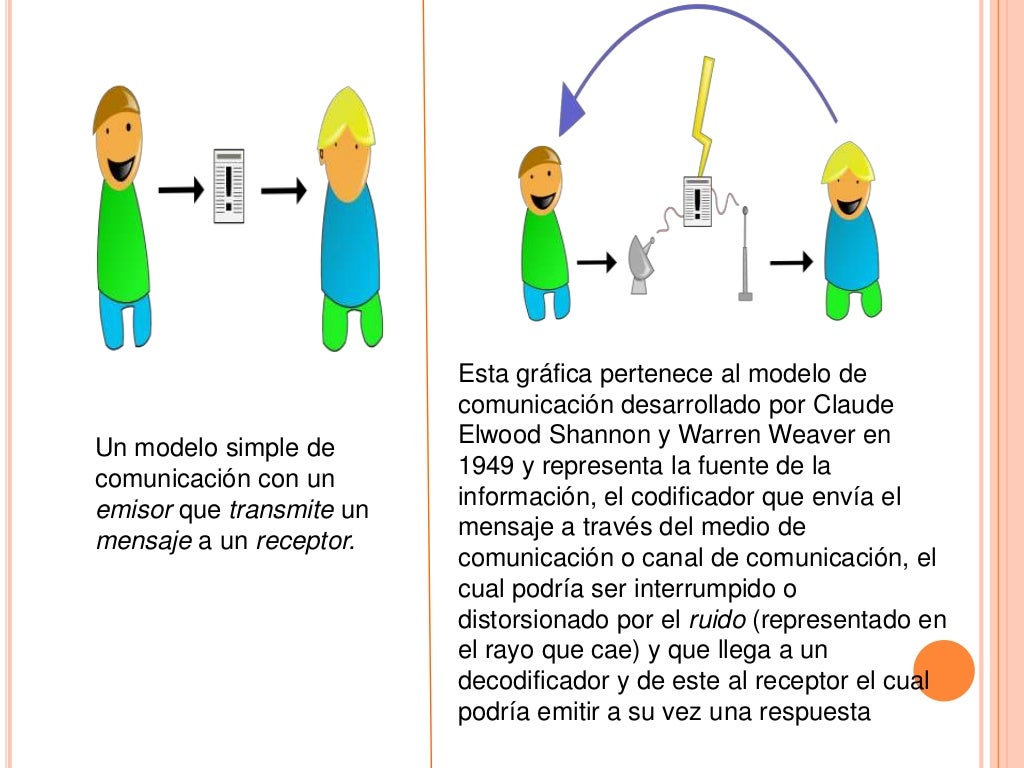
[1]

[1]
Breve Historia de la teoría de Shannon
En 1948, Shannon y Weaver lanzaron una teoría matemática de la comunicación. Su primera versión apareció en el Bell System Technical Journal de octubre de 1948, perteneciente a la Bell Telephone Laboratories, organización a la que Shannon se encontraba procesionalmente ligado.
Poco después el sociólogo Warren Weaver redacto un ensayo destinado a enfatizar las bondades de esta propuesta, que fue publicado junto al texto anterior en julio de 1949. El trabajo de shannon se titula The Mathematical Theory of comunication. [2]
Teorema de Shannon
Sus teoremas más conocidos en la actualidad son el primer y segundo teorema. El primer teorema mejor conocido como codificación sin ruido, el valor de la entropía H(S) de la fuente es igual al número de símbolos necesarios en promedio para codificar una letra de la fuente usando un código ideal: H(S) mide la compresión óptima de los mensajes de la fuente. La prueba del teorema se basa en el hecho de que los mensajes de longitud N que produce S pueden ser clasificados en dos clases. Una de estas clases tiene aproximadamente 2NH(S) mensajes típicos. La otra clase, contiene los mensajes atípicos. Cuando N → ∞, la probabilidad de un mensaje atípico se vuelve despreciable. Por ello, se puede concebir a la fuente como produciendo sólo 2NH(S) mensajes posibles. Esto sugiere una estrategia natural para codificar: cada mensaje típico es codificado en una secuencia binaria de longitud NH(S), que es en general más corta que la longitud N del mensaje original.
La fuente consiste en un sistema S de n estados si, que se pueden pensar como letras de un alfabeto As = {s1,...,sn}, cada una con su propia probabilidad p(si). Las secuencias de letras son llamadas mensajes. La entropía de la fuente H(S) se puede calcular exclusivamente en términos de estos elementos, y se mide en bits cuando el logaritmo tiene base 2. A su vez, el transmisor codifica el mensaje de la fuente y esto equivale a hacer una conversión entre el alfabeto de la fuente As = {s1,...,sn}, y el código del alfabeto del transmisor T, que viene dado por AC = {c1,...,cq}. Los elementos ci son llamados símbolos. La secuencia de símbolos producidos por el transmisor y que entran al canal se llama señal. El alfabeto de n símbolos AS puede variar mucho dependiendo de los distintos dispositivos empleados. Por otro lado, en muchos ejemplos de interés, conviene elegir un AC binario, es decir, con q = 2. En este caso, los símbolos son directamente dígitos binarios. Pero en el caso más general, el alfabeto del código se puede implementar físicamente por medio de sistemas que tengan una cantidad q de estados disponibles. Para el caso particular en que q = 2, los sistemas de dos niveles se pueden llamar cbits.
En el contexto de la teoría de la información de Shannon, codificar implica establecer un mapa entre las letras si del alfabeto de la fuente AS el conjunto de cadenas de longitud finita de símbolos del alfabeto del código AC. Estas suelen llamarse palabras-código. En general, las palabras-código no tienen la misma longitud. Cada palabra-código wi que corresponde a la letra si, va a tener una longitud li. Pero las longitudes li de las distintas palabras-código pueden variar. Es entonces útil definir una longitud de palabra-código promedio como:
L es entonces una medida de cuán compacto es el código. En otras, palabras, un código con un valor de L más pequeño será más eficiente, dado que en promedio, economiza más recursos informacionales para codificar los mensajes. El Teorema del Canal Sin ruido afirma que existe un proceso de codificación óptimo tal que la longitud de palabra-código promedio L está tan cerca como se quiera del límite inferior Lmin para L:
n la fórmula de arriba, si H(S) se mide en bits, log es el logaritmo en base 2.
Es importante enfatizar la diferencia entre el proceso de generación de la información en la fuente y la codificación de la información en el transmisor. La información generada en la fuente se mide con H(S), y sólo depende de las características de la fuente. Puede ser expresada en bits o en cualquier otra medida de la información. Además, la información así generada puede ser codificada mediante un alfabeto código de un número arbitrario de símbolos y la longitud promedio de las palabras código depende esencialmente de ese número. [3]
EL PROBLEMA DE LA CODIFICACIÓN
Shannon estableció resultados matemáticos acerca de los recursos que se necesitan para la codificación óptima y para la comunicación libre de errores. De acuerdo a Shannon ( 1948 ) ( ver también Shannon y Weaver 1949 ), un sistema de comunicación general consta de varias partes. Un transmisor, que transforma el mensaje generado en la fuente en una señal a ser transmitida. En los casos en los que la información es codificada, el proceso de codificación también es implementado por el transmisor. Un canal es cualquier medio que sirva para que la señal se transmita desde el transmisor al receptor. Este puede ser, por ejemplo, un cable, una fibra óptica o una señal inalámbrica.


http://dia.austral.edu.ar/images/9/91/Shannon_1.jpg
S es un sistema que toma diferentes estados S1,.., Sn, shannon nos dice que estos estados pueden ser tomados con probabilidades P(S1),..., P(Sn). La cantidad de información que se genera por la fuente S_i se define.

S produce sucesiones de estados que son llamadas mensajes
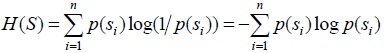
De manera análoga, el destinatario D es un sistema con un rango de estados d_1,..., d_m que también se le asignan probabilidades, la cantidad de información recibida se define como d_j
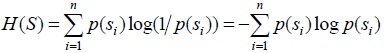
Y la entropia del destinatario se define como
S es un sistema que toma diferentes estados S1,.., Sn, shannon nos dice que estos estados pueden ser tomados con probabilidades P(S1),..., P(Sn). La cantidad de información que se genera por la fuente S_i se define.

S produce sucesiones de estados que son llamadas mensajes
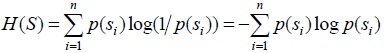
De manera análoga, el destinatario D es un sistema con un rango de estados d_1,..., d_m que también se le asignan probabilidades, la cantidad de información recibida se define como d_j
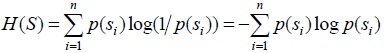
Y la entropia del destinatario se define como
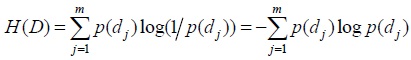
Perspectivas a futuro: Información cuántica
Plantea al mismo tiempo, nuevos interrogantes vinculados a los fundamentos de la ciencias físicas y de la computación ( ver por ejemplo : Duwell 2003 ; Duwell 2008 ; Caves y Fuchs 1996 ; Caves, Fuchs y Schack 2002b ; Deutsch y Hayden 2000 ; Holik, Bosyk y Bellomo 2015 ; Jozsa 1998 ; Jozsa 2004 ; Schumacher 1995 ; Bub 2005 ; Clifton, Bub y Halvorson 2003 ; Nielsen y Chuang 2010 ; Hayashi 2006 ). Respecto de la discusión acerca de la relación entre la Computación Cuántica y el principio de Church - Turing ( que no podemos tratar aquí por una cuestión de espacio ), ver ( Deutsch 1985 ). Es posible encontrar versiones de muchos de los resultados de la toría de Shannon en el conexto no conmutativo de la mecánica cuántica. En especial, existe una versión cuántica del teorema de codificación de Shannon ( Schumacher 1995 ), en el que la codificación se efectúa en términos de sistemas cuánticos de dos niveles, conocidos con el nombre de qubits ( abreviación de quantum bit ). Los qubits constituyen la unidad elemental de información cuántica. En este caso, la medida de información de Shannon, debe ser reemplazada por su versión no conmutativa : la entropía de ( von Neumann, Holik, Plastino y Sáenz ). En general, es posible considerar a la teoría de la información cuántica como una versión no conmutativa ( o no Kolmogoroviana ) de la teoría de la infomación Shanon : es decir, una teoría de la información en la que las medidas de probabilidad involucradas no obedecen a los axiomas de Kolmogorov ( Holik, Bosyk y Bellomo 2015 ). Esto está vinculado con el principio de complementariedad y al carácter contextual de la teoría cuántica ( Renes 2013 ). Estas características peculiares del formalismo cuántico, junto con la noción de entrelazamiento, permiten desarrollar protocolos de información que carecen de análogo clásico, tales como el superdense coding y la teleportación cuántica. El lector interesado en profundizar en estos temas puede consultar la obra clásica de ( Nielsen y Chuang 2010 ). Esta disciplina se basa en el hecho de que no es posible observar a un sistema cuántico sin perturbarlo, para desarrollar protocolos de generación de llaves secretas extremadamente seguros ( Nielsen y Chuang 2010 ). Feynman en 1982 ( ver Feynman 1982 ), pero es también importante tener en cuenta ( Manin 1980 ). Por un lado, están aquellos que se pueden computar en tiempos razonablemente cortos y que consumen recursos que crecen como una funcion polinomial del largo de la entrada del problema a resolver. Es posible demostrar que existen algortimos que permiten resolver ciertos problemas con recursos polinomiales usando computadoras cuánticas, mientras que no existe o no se conoce una version polinomial para resolverlos con computadoras clásicas.El problema comunicacional y la noción de información
En su artículo ‘A mathematical theory of communication’ ( Shannon 1948 ), Shannon introdujo los lineamientos fundamentales sobre los que se construiría posteriormente la Teoría de la Información. En efecto, al comienzo de su artículo, Shannon señala que : Una base para esta teoría está contenida en los importantes artículos de Nyquist y Hartley en este tema. ” ( Shannon 1948 ) ” ( Shannon 1948 ) Uno de los principales aportes de Shannon fue el especificar cuál es el problema informacional, y separar los aspectos formales de los aspectos semánticos asociados con el contenido del mensaje : ” ( Shannon 1948 ) ” ( Shannon 1948 ) De este modo, Shannon define el problema en términos técnicos precisos, separando el problema de ingeniería concreto asociado al proceso de comunicación con los aspectos semánticos de la noción de información vinculados a su uso generalizado en el lenguaje cotidiano. Lo que señala Shannon es simplemente que los aspectos semánticos son irrelevantes para el problema planteado en la ingeniería del proceso comunicacional. El formalismo de Shannon ha sido desarrollado desde diversos enfoques, que poseen un mayor o menor grado de abstracción ( ver por ejemplo : Shannon 1943 ; Shannon 1948 ; Shannon y Weaver 1949 ; Cover y Thomas 1991 ; Khinchin 1957 ; Reza 1961 ; Bell 1957 ). Desde el punto de vista del abordaje Bayesiano a las probabilidades ( Cox 1948 ; Cox 1961 ), es posible encontrar la medida de Shannon desde una perspectiva alternativa ( ver por ejemplo Knuth 2004 ; Knuth 2005a ; Knuth 2005b ; Knuth 2012 ; Goyal y Knuth 2011 ). Este último enfoque se puede extender a modelos probabilísticos más generales, incluyendo la teoría cuántica y la entropía de von Neumann ( Holik, Sáenz, y Plastino 2014 ; Holik, Plastino, y Sáenz 2016 ). Antes de continuar, es importante destacar también que, aparte de la entropía de Shannon, existen otras medidas de la información, como por ejemplo la de Chaitin ( 1987 ), la de Fisher ( Fisher 1925 ), y las entropías de Tsallis y Rényi ( Rényi 1961 ; Tsallis 1988 ; Rastegin 2014 ; Holik, Bosyk, y Bellomo 2015 ) que no discutiremos aquí por razones de espacio.
REFERENCIAS
[1] https://es.slideshare.net/xxjeanxx/modelo-de-comunicacin-shannon
[2] http://algarabiacomunicacion.blogspot.com/2013/04/modelo-de-comunicacion-de-shannon-y.html
[3] http://dia.austral.edu.ar/Teor%C3%ADa_de_la_informaci%C3%B3n_de_Claude_E._Shannon#Los_teoremas_de_Shannon
Video sobre la teoria de shannon.

